【問題一覧】
1. 式の計算
次の問題を解いてみよう
\(\frac{2a+3b}{3} – \frac{3a+2b}{2}\)
2. 角度を求める問題
次の図にある\(x^\circ\)の角度を求めてみよう
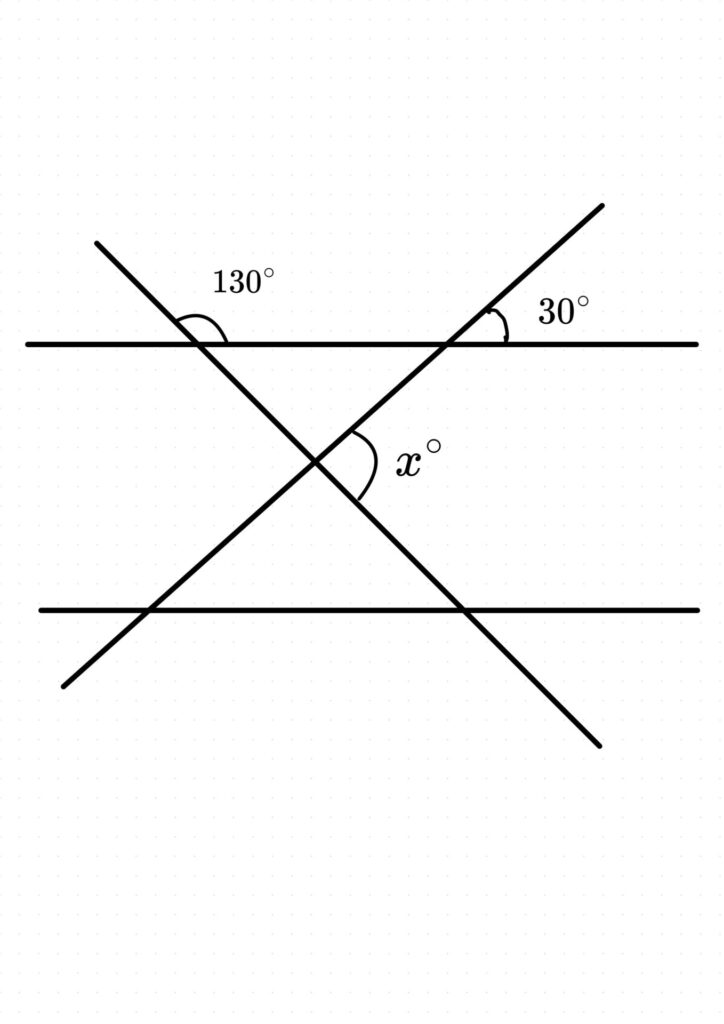
3. 等式変形
等式\(5a+2b=3\)をbについて解いてみよう
4. 座標から式を求める(一次関数)
関数\(y = ax + b\)のグラフが、\((0 , -3) (2, 3)\)を通る。このときの\(a,b\)の値を求めてみよう。
5. 距離・時間・速さの問題
Aさんは家から公園までは毎分\(80\)m、公園から学校までは毎分\(120\)mの速さで歩いた。
家から学校までの道のりは900mで、家から学校まで移動した時間は10分だった。
Aさんの家から公園までの道のり、公園から学校までの道のりをそれぞれ求めてみよう。
【解説】
1. 式の計算
\(\frac{2a+3b}{3} – \frac{3a+2b}{2}\)
この問題は「通分」・「符号の処理」がポイント
まずは\(\frac{(2a+3b)}{3} – \frac{(3a+2b)}{2}\)のように( )を上手に使おう
次は分母を揃えてみよう
\(\frac{2(2a+3b)}{6} – \frac{3(3a+2b)}{6}\)となる
次に( )を外してみよう
\(\frac{4a+6b-9a-6b}{6} \)となる
分子をきれいに並べてみよう
\(\frac{4a-9a+6b-6b}{6} \)となる
これを計算すると
\(\frac{-5a}{6} \)となって、これが答え
解説
計算ミスを減らすためには、( )を積極的に使うことが重要!!
2. 角度を求める問題
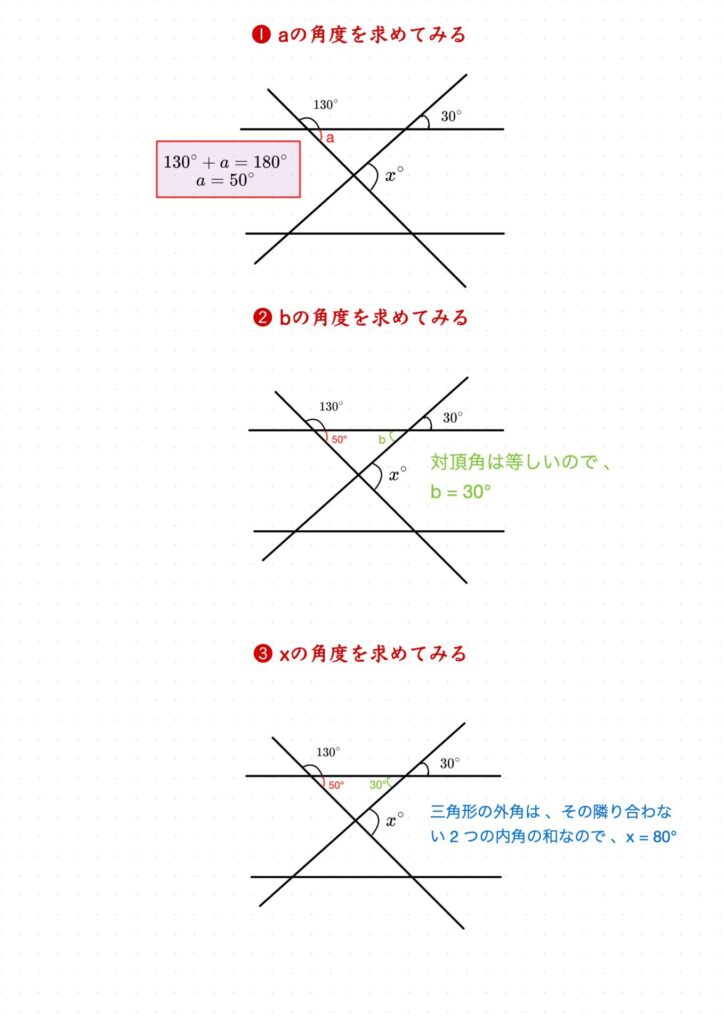
解説
「三角形の外角は、それと隣り合わない2つの内角の和に等しい」は証明においても利用することあります!!
2026年の栃木県の入試で出題されましたので、ぜひとも確認してみましょう!!
3. 等式変形
等式\(5a + 2b = 3\)の\(5a\)を右辺に移項すると、
\(2b = -5a +3\)となるので、
両辺を2で割ると、
\(b = \frac{-5a + 3}{2}\)となる
4. 座標から式を求める(一次関数)
グラフが座標\((0,-3)\)を通るので、\(y=ax+b\)の切片は\(-3\)となる。
よって、\(b=-3\)となる。
\(y=ax-3\)に、\((2, 3)\)を代入すると、
\(3 = 2a -3\)となり、
これを計算すると、
\(a = 3\)となる。
よって、答えは\(a = 3 , b = -3\)
解説
座標(0,☆)を通るということは、切片が☆であると同じ意味であることを覚えておこう!!
5. 距離・時間・速さの問題
まずは求めるものを文字に置き換えることから始めるべきなので、
家から公園までの道のりを\(xm\)、公園から学校までの道のりを\(ym\)としよう。
道のりについて考えてみると、
家から学校までの道のりが\(900m\)なので、
\(x + y = 900\)…①と置くことができる。
次に時間について考えてみると、
家から公園までは毎分\(80\)m、公園から学校までは毎分\(120\)mの速さで、
家から学校までの移動時間が10分なので、
\(\frac{x}{80} + \frac{y}{120} = 10\)…②となる。
①と②より、
\(\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = 900…① \\
\frac{x}{80} + \frac{y}{120} = 10…②
\end{array}
\right.
\end{eqnarray}\)
②の両辺に240をかけると、
\(3x + 2y = 2400\)となるので、
これに①をyについて変形した\(y = 900 – x\)を代入すると、
\(3x + 2(900-x) = 2400\)となるので、
これを展開すると、
\(3x + 1800 -2x = 2400\)となり、
これを計算すると、
\(x = 600\)となる
\(x = 600\)を①に代入すると、
\(y = 300\)となる。
よって答えは
家から公園までの道のりが600m
公園から学校までの道のりが300m
解説
このタイプの問題は「道のりの式」と「時間の式」をそれぞれ作り上げることで解けるので、その方向性で考えてみよう!!



